Uniswap v2/v3 Simulator
tl;dr: just let me play with the simulator! => Uniswap v2/v3 simulator
This document shows how to use my Uniswap v2/v3 model (AMM DEX Simulator), the best way to understand basics of DeFi. Actually , many other DEX are forked from Uniswap v3, like Sushiswap and PancakeSwap.
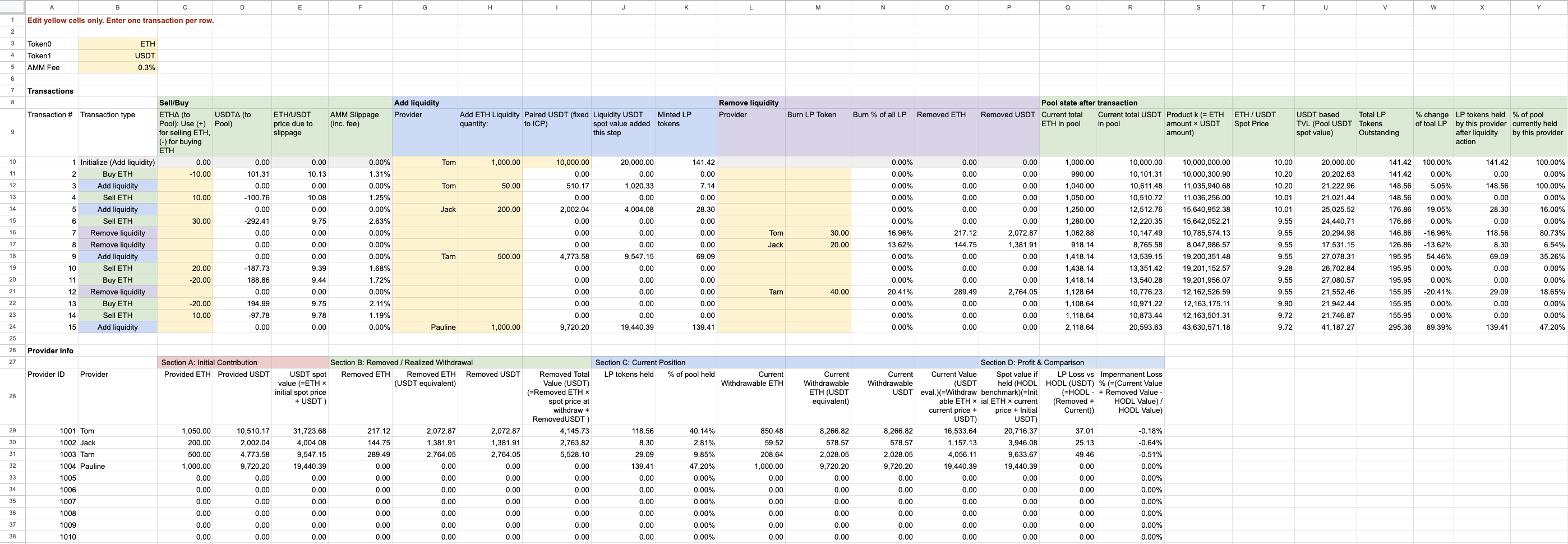
If you are new to DeFi, I recommend playing with Uniswap v2 sheet and read Uniswap v2 Simulator Guide, since v2 is the foundation of all the DeFi logics. You'll grab what the famous 'x * y = k' means, how the price is determined, and why slippage happens. In the v3 simulator, we focus on LP and ignore swaps. This will allow you to understand what concentrated liquidity model means, and the importance of price range when adding LP.
Uniswap v2 Simulator Guide
Uniswap v2 sheet explains the basics of Uniswap v2's constant product AMM model. The sheet allows you to simulate real-world v2 swaps, liquidity provision, and understand LP rewards and slippage.
🔍 What is Uniswap v2?
Uniswap v2 is a decentralized exchange protocol that introduced the constant product formula to enable token swaps without an order book for the first time. It operates under the formula:
x * y = k
Where:
x= amount of Token0 in the pool (e.g., ETH)y= amount of Token1 in the pool (e.g., USDT)k= a constant, preserved during swaps
Isn't it beautiful?
About the Simulator
The sheet titled Uniswap v2 models how the pool state evolves as users perform swaps and liquidity actions.
Initial Setup:
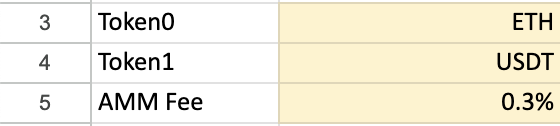
You can modify those labels and numbers, then start simulating transactions by entering one per row under the transaction table.
Transaction Types
Each row represents one transaction. The supported types include:
| Type | Description |
|---|---|
Initialize (Add liquidity) |
Creates the initial pool state |
Add liquidity |
Adds Token0/Token1 pair to the pool |
Remove liquidity |
Withdraws LP tokens and returns assets |
Buy token0 / Sell token1 |
Executes a swap in either direction |
In Uniswap v2 model (and also v3), initial pool state decides the starting price in AMM. You will see how easy to manipulate the initial price in DeFi, when the liquidity is minimum.

The username is just for visualization purpose. In AMMs, it's usually a wallet address.
Key Outputs Calculated
| Column | Description |
|---|---|
token0/token1 price due to slippage |
Execution price after accounting for slippage |
AMM Slippage (inc. fee) |
Total price impact including LP fee |
Pool state after transaction |
token0/token1 reserves after each action |
k = x * y |
Constant product for internal consistency |
LP Tokens Outstanding |
Total LP tokens in circulation |
Pool Ownership % |
Share held by each LP |
In v2 models, all the fees are just thrown into the LP pool for each token pair, luke a big bathtub.
Learning Outcomes
1. Price Discovery is Automatic
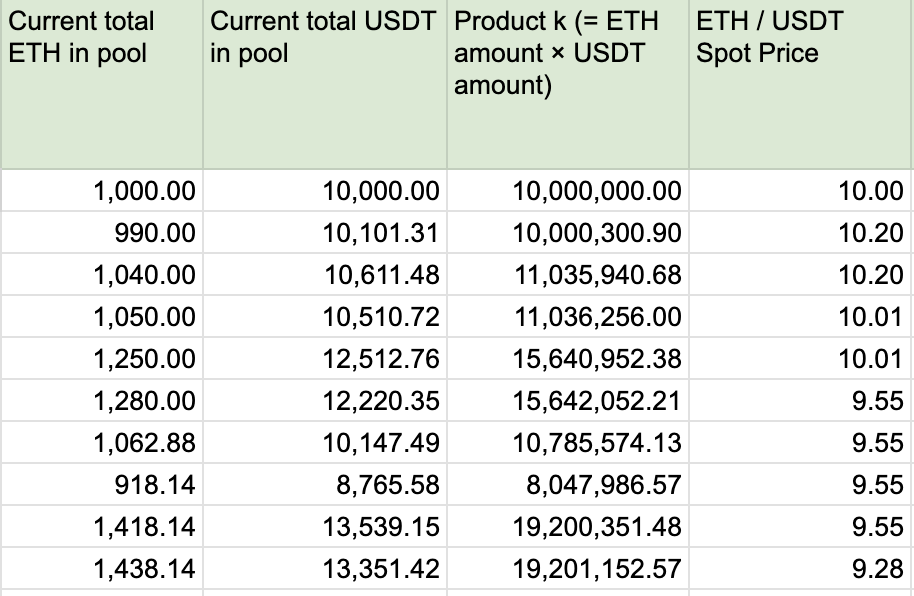
Prices are determined by the ratio of token reserves. A swap of Token0 into the pool pushes up Token0's reserve and decreases Token1's, moving the price accordingly.
2. Slippage Depends on Pool Depth
Larger swap amounts relative to pool size result in higher slippage.
For example, buying 10 ETH from a 1000 ETH pool results in moderate slippage. Buying 500 ETH would drastically impact the price.
3. LPs Earn from Swap Fees
Each swap incurs a fee (i.e. 0.3%), which accrues to the liquidity pool, increasing the total value of LP tokens.
4. LP Tokens Represent Share of the Pool
When liquidity is added, LP tokens are minted proportionally. When removed, they're burned to return the LP's share of the reserves.
Experiment Ideas
Make your copy of GSS, and try simulating the following:
- Execute multiple swaps and observe how the spot price and k-value evolve
- Add and remove liquidity at different pool states
- Track LP share and see how fee income accumulates over time
Formula Recap: How a Swap Works
To compute a swap, the simulator uses the invariant:
(x + Δx) * (y - Δy) = k
Solving for Δy (output token received), taking into account the fee:
Δx_net = Δx * (1 - fee)
Δy = y - (k / (x + Δx_net))
Uniswap v3 Simulator Guide
This document explains the mechanics of Uniswap v3's concentrated liquidity model using Google Spreadsheet: Uniswap v3 (Single LP, Static Position) and v3 Virtual Liquidity by Tick. The simulator allows you to visually understand how liquidity provision and price movement work in v3.
What is Uniswap v3?
Uniswap v3 is a new DEX model debut in 2021, which evolved the traditional AMM (Automated Market Maker) model by introducing the concept of concentrated liquidity.
Key Features:
- Liquidity providers (LPs) can specify the price range in which their funds are active
- Much higher capital efficiency than v2
- Liquidity density varies depending on the price range
About the Uniswap v3 (Single LP, Static Position) Sheet
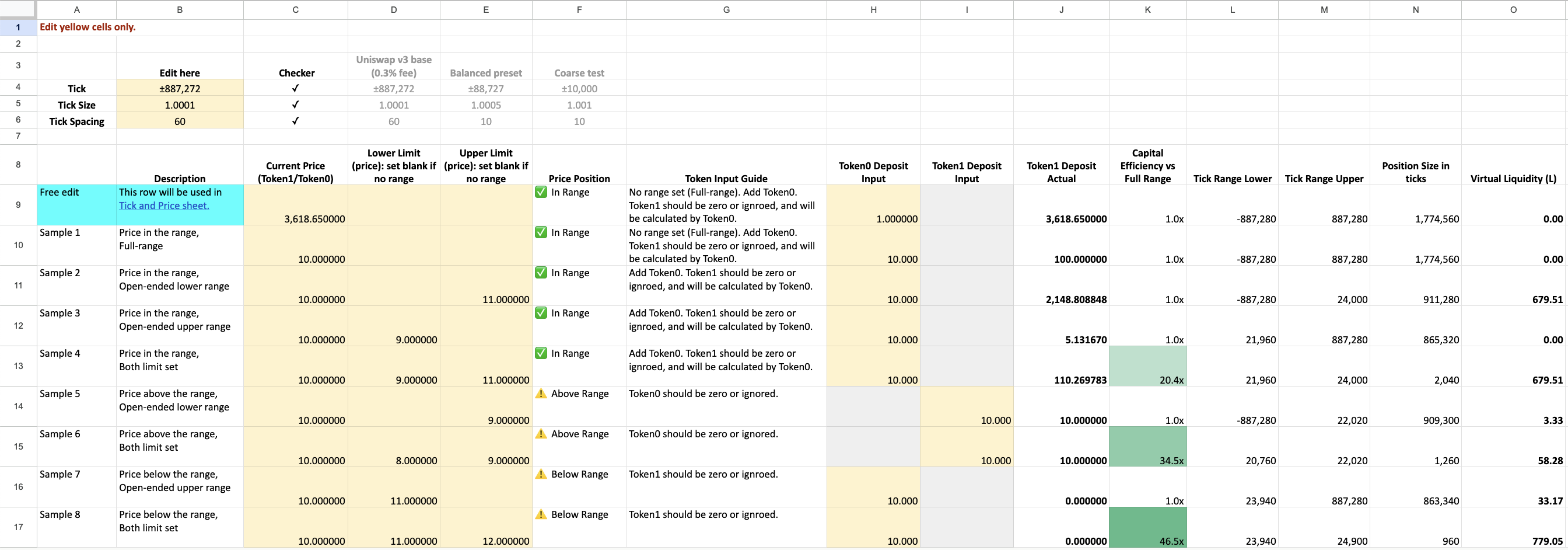
In this Uniswap v3 (Single LP, Static Position) simulator, you can configurate Tick/Tick Size/Tick Spacing.
| Parameter | Description |
|---|---|
| Tick | Distance from base tick. Defines the total price range. |
| Tick Size | Price multiplier per tick. Smaller = finer price granularity. |
| Tick Spacing | Interval between allowed liquidity positions. Smaller = more flexibility. |

Then, you can start simulating how different LPs provide liquidity with various strategies. Key input items include:
| Field | Description |
|---|---|
Lower Limit / Upper Limit |
Price range in which the LP provides liquidity |
Token0 Deposit Input |
Amount of Token0 deposited (e.g., ETH) |
Token1 Deposit Actual |
Calculated amount of Token1 needed (e.g., USDT) |
Price Position |
Indicates whether the current price is within the LP's active range |
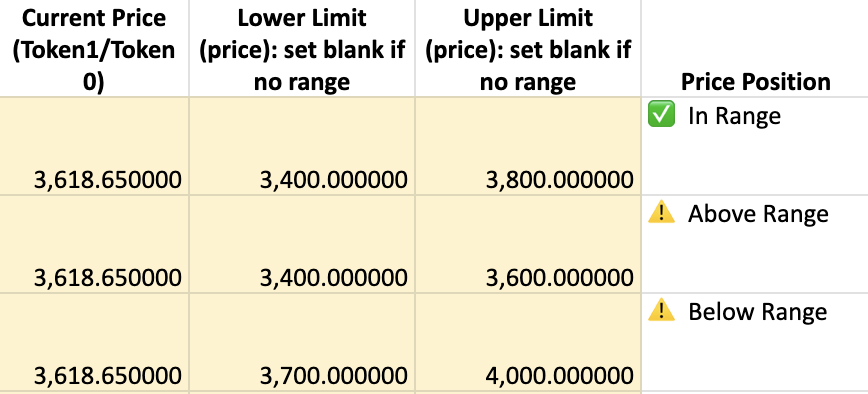
✅ If "In Range": the LP is actively participating and earns fees
⚠️ If "Out of Range" (Above/Below): the LP is inactive and earns no fees
Virtual Liquidity (L) and Price Ticks
In Uniswap v3, the liquidity provided (L) is not spread across the price range. Instead, it only becomes active when the current price falls within the LP’s specified range.
Important Behavior:
- Only one price tick is active at any given time (based on the current price)
- The same L cannot be active across multiple ticks simultaneously
- As the price moves during swaps, L slides to the next tick, one at a time
What v3 Tick and Price Sheet Shows
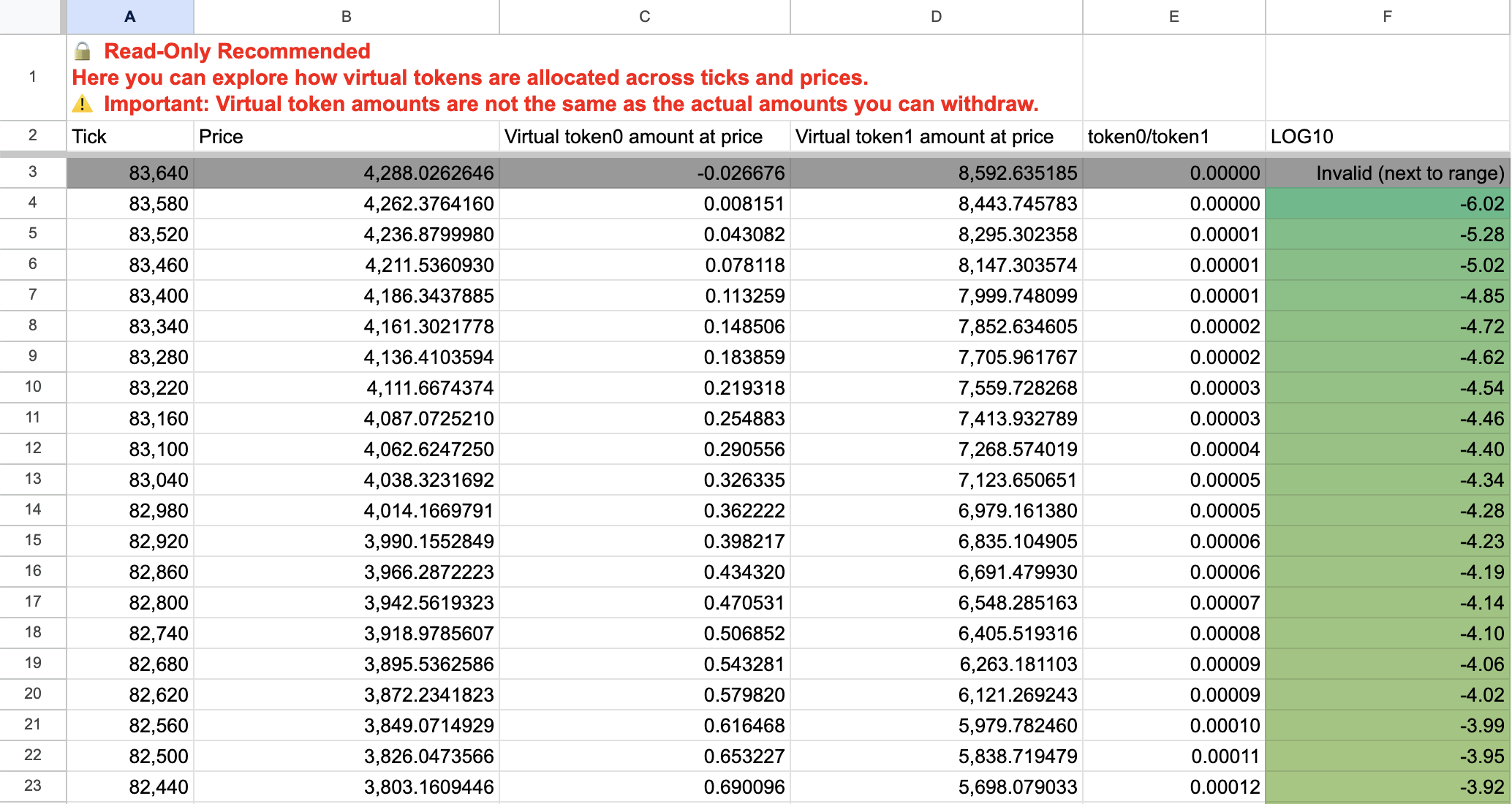
v3 Virtual Liquidity by Tick outputs a snapshot of what virtual liquidity would look like if the price were located at each tick.
| Column | Meaning |
|---|---|
Tick |
Uniswap v3 price slot (integer) |
Price |
Price converted from tick (1.0001^tick) |
Virtual token0/token1 amount |
Amount of virtual liquidity active at that tick |
token0/token1 |
Swap rate at that tick |
LOG10 |
logarithmic view of the relative proportion between token0 and token1 |
If you modify the price range on Uniswap v3 (Single LP, Static Position), you'll know the importance of price range by looking at each row on this sheet. If no ranges, you'll end up seeing something like this. You add almost zero liquidity for the most ticks/prices.
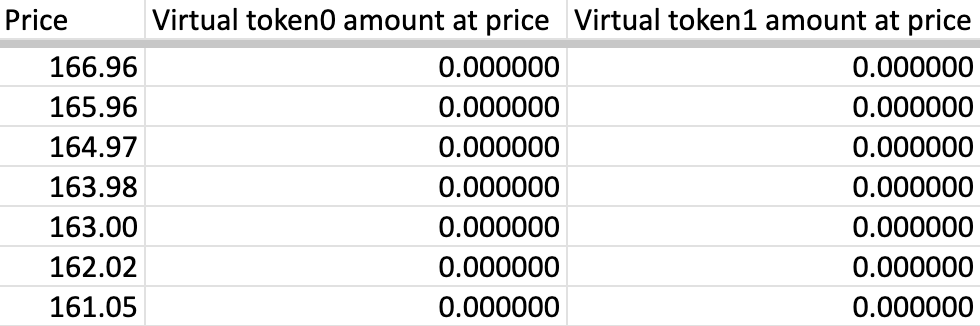
Clarification:
- LPs do not directly deposit liquidity into specific ticks
- This sheet assumes: "What if the current price was at this tick?" and calculates virtual liquidity accordingly
Intuition: One Tick at a Time
In Uniswap v2, liquidity is shared across the entire price curve — like everyone putting money into one big bathtub.
In Uniswap v3, each LP builds their own canal (price range). However, the water (liquidity) only flows in the canal that matches the current price.
💬 “Water can only flow through one canal at a time.”
That’s the essence of v3.
Try Out v3 Strategies in GSS
- Narrow price range (e.g., 3000–3100): highly efficient, but risk of being inactive if price moves
- Wide price range (e.g., 2000–5000): always active, but less fee income per dollar
This simulator helps you experiment with different LP strategies and visualize their outcomes.
Summary
| Concept | Explanation |
|---|---|
| Concentrated Liquidity | LPs target specific price ranges |
| Active Range | Liquidity is only active when price is within the range |
| Virtual Liquidity (L) | Only applies to the current price tick |
| Tick ↔ Price | Price = 1.0001^tick (exponential relationship) |
References
- Uniswap v2 Whitepaper
- Uniswap Docs: V2 Core
- Uniswap v3 Whitepaper
- Uniswap Docs: V3 Core
- Let's run on-chain decentralized exchanges the way they were meant to be
- Improving front-running resistance of x*y=k market makers (ethresear.ch)
- Excel Liquidity Pool Simulator by kupietools (GitHub)
- Desmos AMM Visual Calculator
- Uniswap Official Documentation
- Uniswap v3 Math Primer (Blog)
- Uniswap v3 Math Primer Part 2 (Blog)
- v2/v3 math (for external use)